How to calculate the synchronous orbits of the planets?
The synchronous orbit planets is calculated using the law of universal gravitation which boils down to: h=√3(G*M*T2/4π2)-R
h = Height of the artificial satellite
G = Constant of gravitation (6.67*10-11)
M = Mass of the planet
T = Rotational period of the planet
R = Radius of the planet
The geosynchronous orbit (synchronous orbit of the Earth) is at an altitude of 35,796 km (≈ 36,000 km) and has a semi-major axis of 42,167 km.
Excel formula used in this table to calculate the altitude of the satellite in synchronous orbit of the planet:
=((((G*M*T^2)/(4*PI()^2))^(1/3))-R*1000)/1000
Excel formula used to calculate the semi-major axis of the synchronous orbit of the planet:
=((((G*M*T^2)/(4*PI()^2))^(1/3)))/1000
- Kerbal Space Program Geostationary Orbit
- Kerbal Stationary Orbit
- Ksp Kerbin Geostationary Orbit Altitude
Kerbal Space Program Geostationary Orbit
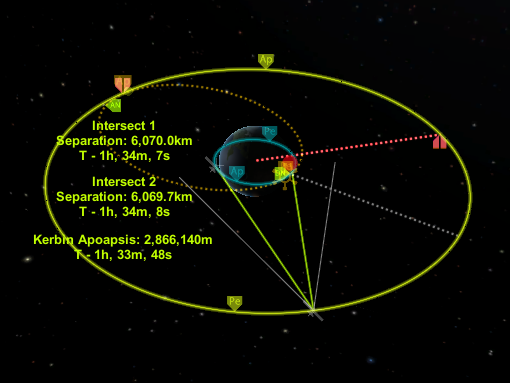
Kerbal Stationary Orbit
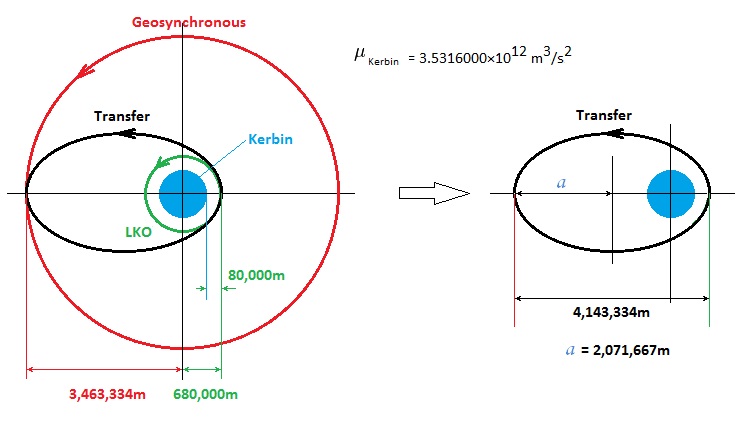
Ksp Kerbin Geostationary Orbit Altitude
If you have one satellite in polar orbit and one in equatorial orbit at a high enough distance (not sure exactly, somewhere around 1000km, maybe more) they will rarely lose contact with each other, and you will always have 360 degree relay coverage, forgoing the need for geostationary orbit networks. Even Matt Lowne says that geostationary orbit around Kerbin is useless since there are antennas everywhere on the surface. The only use I see is for foreign bodies communication system but most of them have the geosynchronous orbit outside of the SOI. The people of twitter hath spoken, I present ye with a guide/playthrough for establishing relays at Kerbin, Minmus and Mun in 1 launch, with the Kerbin and M.
