Avogadro’s number is the number of particles that are present in one mole of a substance. This number is given as a value (in standard form or scientific notation) of 6.02 x 10 23 mol -1 to three significant figures. Contrary to the beliefs of generations of chemistry students, Avogadro’s number—the number of particles in a unit known as a mole—was not discovered by Amadeo Avogadro (1776-1856). About Press Copyright Contact us Creators Advertise Developers Terms Privacy Policy & Safety How YouTube works Test new features Press Copyright Contact us Creators.

Learning Objective

• Convert between the number of moles and the number of atoms in a given substance using Avagadro’s number

Key Points

• Avogadro’s number is a very important relationship to remember: 1 mole = [latex]6.022times10^{23}[/latex]atoms, molecules, protons, etc.
• To convert from moles to atoms, multiply the molar amount by Avogadro’s number.
• To convert from atoms to moles, divide the atom amount by Avogadro’s number (or multiply by its reciprocal).

Terms

• moleThe amount of substance of a system that contains as many elementary entities as there are atoms in 12 g of carbon-12.
• Avogadro’s numberThe number of atoms present in 12 g of carbon-12, which is [latex]6.022times10^{23}[/latex] and the number of elementary entities (atoms or molecules) comprising one mole of a given substance.

Moles and Atoms

As introduced in the previous concept, the mole can be used to relate masses of substances to the quantity of atoms therein. This is an easy way of determining how much of one substance can react with a given amount of another substance.

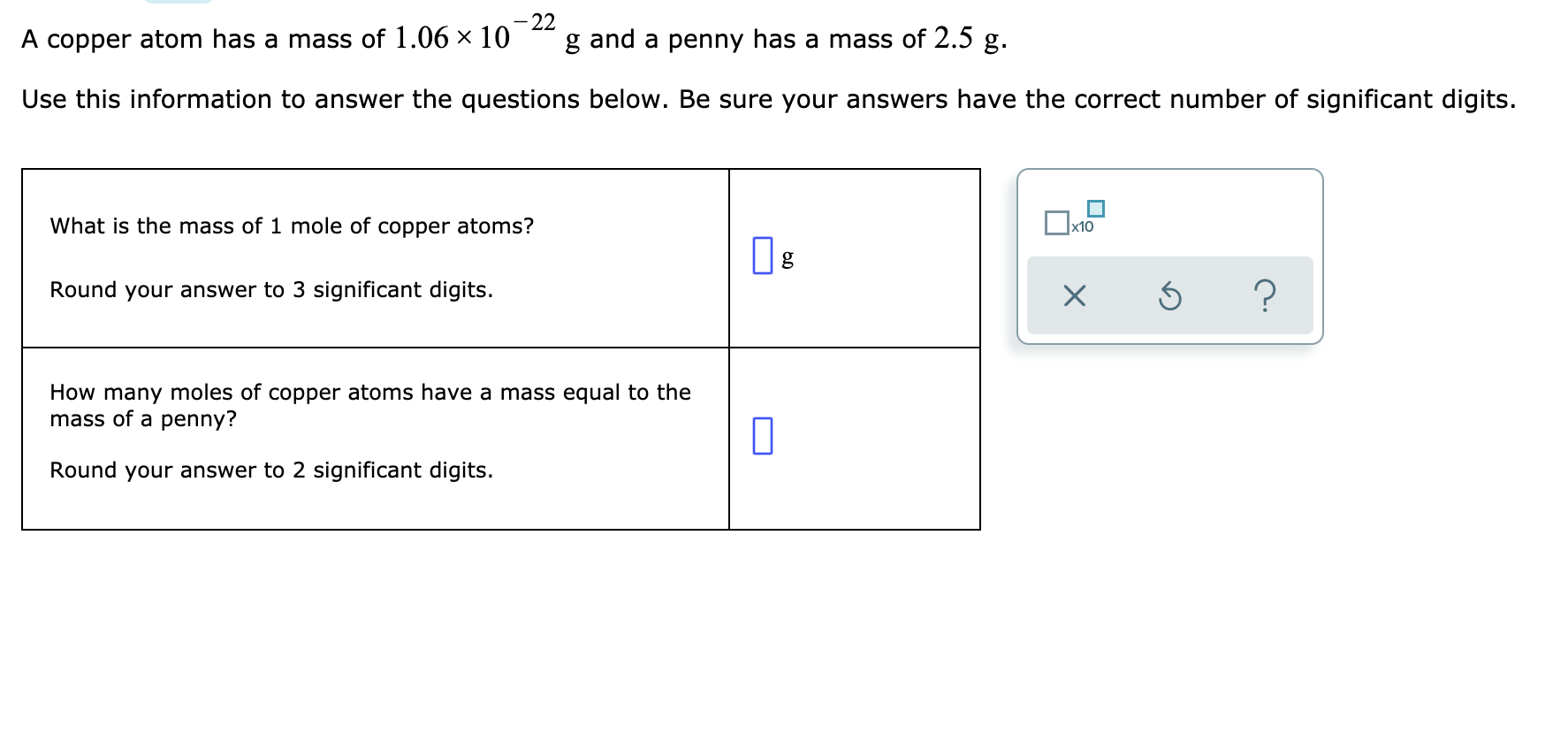
From moles of a substance, one can also find the number of atoms in a sample and vice versa. The bridge between atoms and moles is Avogadro’s number, 6.022×10²³.

Avogadro’s number is typically dimensionless, but when it defines the mole, it can be expressed as 6.022×10²³ elementary entities/mol. This form shows the role of Avogadro’s number as a conversion factor between the number of entities and the number of moles. Therefore, given the relationship 1 mol = 6.022 x 10²³ atoms, converting between moles and atoms of a substance becomes a simple dimensional analysis problem.

Converting Moles to Atoms

Given a known number of moles (x), one can find the number of atoms (y) in this molar quantity by multiplying it by Avogadro’s number:

[latex]x moles cdot frac {6.022times10^{23} atoms}{1 mole} = y atoms[/latex]

For example, if scientists want to know how may atoms are in six moles of sodium (x = 6), they could solve:

$30 copay after deductible. [latex]6 moles cdot frac {6.022times 10^{23} atoms}{1 mole} = 3.61times 10^{24} atoms[/latex]

Note that the solution is independent of whether the element is sodium or otherwise.

Converting Atoms to Moles

Reversing the calculation above, it is possible to convert a number of atoms to a molar quantity by dividing it by Avogadro’s number:

[latex]frac{x atoms}{6.022times 10^{23} frac{atoms}{1 mole}} = y moles[/latex]

This can be written without a fraction in the denominator by multiplying the number of atoms by the reciprocal of Avogadro’s number:

[latex]x atoms cdot frac{1 mole}{6.022times 10^{23} atoms} = y moles[/latex]

For example, if scientists know there are [latex]3.5 cdot 10^{24} [/latex]atoms in a sample, they can calculate the number of moles this quantity represents:

[latex]3.5 times 10^{24} atoms cdot frac{1 mole}{6.022times 10^{23} atoms} = 5.81 moles[/latex]

Boundless vets and curates high-quality, openly licensed content from around the Internet. This particular resource used the following sources:

http://www.boundless.com/
Boundless Learning
CC BY-SA 3.0.

http://en.wiktionary.org/wiki/mole
Wiktionary
CC BY-SA 3.0.

http://en.wikipedia.org/wiki/Avogadro’s%20number
Wikipedia
CC BY-SA 3.0.

http://en.wikipedia.org/wiki/Avogadro_constant
Wikipedia
CC BY-SA 3.0.

From Academic Kids

Avogadro's number, also called Avogadro's constant (N_A) is a large constant used in chemistry and physics.

Definition

Avogadro's number is formally defined as the number of carbon-12 atoms in 0.012 kg of carbon-12. It is approximately 6.022 × 10²³ particles/mole. Historically, carbon-12 was chosen as the reference substance because its atomic mass could be measured particularly accurately.

A mole is defined as Avogadro's number of particles of any kind of substance (atoms, ions, molecules, or formula units).

History

Avogadro's number is named after the early 19th century Italian scientist Amedeo Avogadro.It appears that Jean Baptiste Perrin was the first to name it.Perrin called it 'Avogadro's constant' and it is still sometimes known by that name. The numerical value was first calculated by Johann Josef Loschmidt in 1865 using the kinetic gas theory. In German-speaking countries, the number may still be referred to as Loschmidt's number. Unfortunately, in a few cases (mainly in the older literature) Loschmidt's number refers to the number of atoms (or molecules) in a cubic centimeter, a usage now disparaged, viz: [1] (http://gemini.tntech.edu/~tfurtsch/scihist/loschmid.html)

Application

Avogadro's number can be applied to any substance. It corresponds to the number of atoms or molecules needed to make up a mass equal to the substance's atomic or molecular mass, in grams. For example, the atomic mass of iron is 55.847 amu, so Avogadro's number of iron atoms (i.e. one mole of iron atoms) have a mass of 55.847 g. Conversely, 55.847 g of iron contains Avogadro's number of iron atoms. Thus Avogadro's number corresponds to the conversion factor between grams (g) and atomic mass units:

<math>1 mbox{g}=N_{rm A} mbox{amu}.<math>

Physical significance of Avogadro's number

The value of Avogadro's number depends on the definition of the mole, which depends on the definition of the kilogram. Both definitions, especially that of the kilogram, are arbitrary: the kilogram system is currently based on the mass of a particular 'standard' bar of metal in France. Clearly, this means that the value of Avogadro's number is less fundamental than other physical constants in the sense that there is no physical reason for its particular value. However, Avogadro's number is still a fundamental constant: all constants depend on the units used and on the definition of the units, and therefore, such a dependence does not exclude that a constant can be called fundamental.

Avogadro's number can be regarded as a conversion factor between the microscopic mass system (atomic mass units or Daltons) and the kilogram system. The microscopic mass system is based on the mass of carbon-12, while the kilogram system is currently based on the mass of a particular 'standard' bar of metal in France. So naturally there's no simple conversion factor between the two. However, if a method were developed to count atoms, it would be possible to redefine the kilogram in a way that did not depend on an arbitrary bar of metal. The number of atoms picked would presumably be equal or close to the latest accepted value of Avogadro's number. In that case, the kilogram would be redefined as the mass of 1/0.012=83.333 times Avogadro's number of Carbon atoms.

Additional physical relations

Because of its role as a scaling factor, Avogadro's number provides the link between a number of useful physical constants when we move between an atomic mass scale and a kilogram (SI) scale.For example, it provides the relationship between:

• the universal gas constant R and the Boltzmann constant k: R = k_B N_A
• the Faraday constant F and the elementary charge e: F = e N_A

In the 19th century physicists measured the mass of one atom of hydrogen to be about 1/(6.023x10²³) grams. The gram was originally defined to be the mass of a cubic centimeter of pure water at standard temperature and pressure [2] (http://www.factmonster.com/ce6/sci/A0832931.html). As experiments became more accurate, it was found that water was contaminated with variable amounts of heavy water, which made it undesirable to maintain a standard with hydrogen having one a.m.u. (atomic mass unit). Carbon was found to have a more constant isotopic composition, and it was also possible to separate pure carbon-12. Therefore, the atomic mass unit was changed to 1/12 the mass of an atom of carbon-12 . Hence 12 grams of carbon-12 has about 6.02214x10²³ atoms. The recent history and more details can be found in the document, Atomic Weight: The Name, Its History, Definition and Units (http://www.iupac.org/publications/pac/1992/pdf/6410x1535.pdf).

Numerical value

At present it is not technologically feasible to count the exact number of atoms in .012 kg of carbon-12, so the precise value of Avogadro's number is unknown. The 2002 CODATA recommended value for Avogadro's number is

<math>6.0221415(10)times 10^{23}hbox{ mol}^{-1},<math>

Lg blu ray drive software. where the number in parentheses represents the one standard deviation uncertainty in the last digits of the value.

A number of methods can be used to measure Avogadro's number. One modern method is to calculate Avogadro's number from the density of a crystal, the relative atomic mass, and the unit cell length determined from x-ray crystallography. Very accurate values of these quantities for silicon have been measured at the National Institute of Standards and Technology (NIST) and used to obtain the value of Avogadro's number.

Connection to masses of protons and neutrons

A carbon-12 atom consists of 6 protons and 6 neutrons (which have approximately the same mass) and 6 electrons (whose mass is negligible in comparison). One could therefore think that N_A is the number of protons or neutrons that have a mass of 1 gram. While this is approximately correct, the mass of a free proton is 1.00727 amu, so a mole of protons would actually have a mass of 1.00727 g. Similarly, a mole of neutrons has a mass of 1.00866 g. Clearly, 6 moles of protons combined with six moles of neutrons would have a mass greater than 12 g. Chemical engineeringall engineering e books for free . So, you might ask how one mole of carbon-12 atoms, which should consist of 6 moles each of protons, neutrons, and electrons could possibly have a mass of only 12 g? What happened to the excess mass? The answer is related to the equivalence of matter and energy discovered by Albert Einstein as part of the theory of special relativity. When an atom is formed, the protons and neutrons in the nucleus are bound together by the strong nuclear force. This binding results in the formation of a low energy state and is accompanied by a large release of energy. Since energy is equivalent to mass, the released energy corresponds to a loss in the mass of the nucleus relative to that of the separated protons and neutrons. Thus, protons and neutrons in the nucleus have masses that are less (about 0.7 percent less) than free protons and neutrons. The precise amount of mass loss is related to the binding energy of the nucleus and varies depending on the type of atom.

One may therefore say that N_A is approximately the number of nuclear neutrons or protons that have a mass of 1 gram. This is approximate because the precise mass of a nuclear proton or neutron depends on the composition of the nucleus. For example, iron nucleons will have a significantly lower mass than those in hydrogen or plutonium.

Avogadro's number in life

Avogadro's number often yields practical reasonings in real life. For example, the fact that a known number of atoms are in a given amount of a substance is one reason for scientific criticism of homeopathy, in which medicinal substances are often diluted to the extent that a simple calculation involving Avogadro's number would imply that less than a single molecule remains.

See also

Further reading

Using Avogadro's Number And Molar Masses

• Journal of Physical and Chemical Reference Data, 28 (1999) 1713.

External links

• Some Notes on Avogadro's Number, 6.022 x 10²³ (http://gemini.tntech.edu/~tfurtsch/scihist/avogadro.htm)(historical notes)
• 2002 CODATA value of Avogadro's number at NIST site (http://physics.nist.gov/cgi-bin/cuu/Value?na|search_for=avogadro)ca:Nombre d'Avogadro

Avogadro's Number Times 2